Albert Einstein called compound interest “the greatest mathematical discovery of all time.”
“Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn't … pays it.” Albert Einstein
As we near the close of 2015, I felt this article on the power of compounding may be of some help for those still developing trade plans and capital allocation for next year.
The wonder of compounding (sometimes called “compound interest”) transforms your working capital into a state-of-the-art, highly powerful income-generating tool. Compounding is the process of generating earnings on an asset's reinvested earnings. To work, it requires two things: the re-investment of earnings and time. The more time you give your investments, the more you are able to accelerate the income potential of your original investment, which takes the pressure off of you.
Ben Franklin let his money compound quietly for 200 years?
Here’s an excerpt from the book The Elements of Investing: (written by Burton Malkeil and Charles Ellis)
“Benjamin Franklin provides us with an actual rather than a hypothetical case. When Franklin died in 1790, he left a gift of $5,000 to each of his two favorite cities, Boston and Philadelphia. He stipulated that the money was to be invested and could be paid out at two specific dates, the first 100 years and the second 200 years after the date of the gift. After 100 years, each city was allowed to withdraw $500,000 for public works projects. After 200 years, in 1991, they received the balance—which had compounded to approximately $20 million for each city. Franklin’s example teaches all of us, in a dramatic way, the power of compounding. As Franklin himself liked to describe the benefits of compounding, “Money makes money. And the money that money makes, makes money”.
To demonstrate compound interest, let's walk through an example:
- Position with $20,000 allocated capital
- Average return 5% per month for the year, including losses
- Reinvest 100% of the proceeds each month.
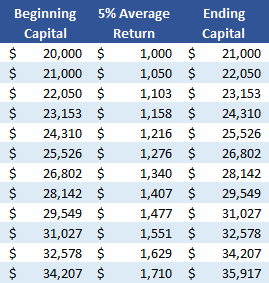
At the end of 12 months, your original $20,000 allocated capital has now increased to $35,914. This is a gain of $15,914, or 80% return on your original capital.
This increase in the amount of capital each year is compounding in action: profits earning profits. This will continue as long as you keep reinvesting 100% of your gains.
But what if I want to draw a portion of my profits?
Most traders, at least those who trade full time for income, draw from their profits to meet income goals. To keep it simple, I'll use the same example as above, only adding a monthly draw to the equation.
- Position with $20,000 allocated capital
- Average return 5% per month for the year, including losses
- Instead of reinvesting 100% of the proceeds each month, half the average return is drawn each month (2.5%)
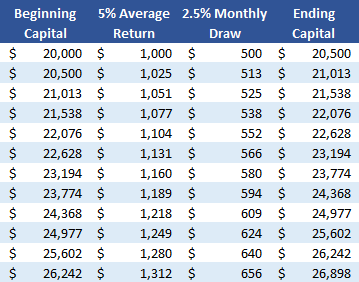
In this second example, at the end of 12 months your original $20,000 capital allocation has now increased by $6,899 to $26,899, or 34% of your original capital allocation. Also, the 2.5% monthly draw increases as your reinvestment of capital compounds from $500 to $656 at the end of 12 months.
Whether you are able to re-invest 100% of your profits, or only a portion, always keep in mind that compounding amplifies the growth of your working capital. Just like investing maximizes your earning potential, compounding maximizes the earning potential of your trading investments.
Would you like to calculate approximately how long it would take for your money to double using compound interest?
Use the rule of 72. Take 72 and divide it by the expected return. The number you derive from the calculation will determine approximately how long it will take for your money to double.
Let's use a couple of examples:
In the first example we have an expected return of 6% per month. Take 72 and divide it by 6 and you get 12 months to double your money.
In the second example let's say the expected return is 5% per month. Take 72 and divide it by 5 and you get 14.4. So it would take approximately 14.4 months to double your money.
Now let's say you trade weeklies.
You are a great weeklies trader, and you average 4% profit per week. Take 72 and divide it by 4 which equals 18. So it would take approximately 18 weeks to double your money, using the average return of 4% per week.
Whatever trade strategy you use and your overall trading goals, the power of compounding is one more tool in your kit. Don't have your own trading style yet? Adapt one of the trade strategies offered by capitaldiscussion.com into your plan.
I am sure you can see from the examples shown in this article how the magic of compound interest can add up quickly. If you are able, wouldn't it be great to let one of your accounts grow from compound interests' magic next year? Feel free to comment below.



Nice article however the last section examples have some typos switching months for years.
Thanks very much for bringing that to my attention, Rick – That slipped by in my last proofreading.
Joanna